1. 题意概述

354. 俄罗斯套娃信封问题。

信封尺寸由两个整数$(w, h)$描述，分别表示宽和高。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

给定一系列信封的尺寸，计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

注意：不允许旋转信封。

2. 解法

这道题本质上是个最长上升子序列（Longest Increasing Subsequence, LIS）问题。

LIS问题基本上都是用动态规划（Dynamic Programming, DP），时间复杂度$O(N^2)$；优化后时间复杂度可以达到$O(NlogN)$。

这道题也是一样。不过，由于要求“严格小于”而不是“小于等于”，略微有点难度。

2.1. 朴素DP

首先将信封按照宽度$w$从小到大排序，如果$w$相等则随便排。

对于信封$E_1$、$E_2$、……、$E_{k-1}$中每一个信封$E_i$，都求出以$E_i$为最大信封，能达成的最长俄罗斯套娃信封（下称“信封链”，其中最大的信封称为“末端信封”）的长度$L_i$。

那么对于当前信封$E_k$，遍历前面的$k-1$个信封。

  • 如果$E_k$的长和宽都严格大于$E_i$，就能形成一个长度为$L_i+1$的信封链。
  • 否则，就只能靠$E_k$生成长度为$1$的信封链了。

于是，只要遍历前$k-1$个信封，按照上面的方式算出$k-1$个“以$E_k$为末端信封的信封链长度，其中最大的那个，就是$L_k$。

时间复杂度：$O(N^2)$。

2.2. 优化DP

对于若干信封，比如$E_a$、$E_b$、$E_c$，如果$L_a = L_b = L_c$，那么在计算$L_k$时其实没必要比较这3个信封，而只需要比较其中“最小的”那个信封（称其为$E_{min}$）。

  • 如果$E_{min}$能放进$E_k$里面，则$L_{min}+1$就是$L_k$的一个候选值，没必要再比较另外两个信封了（反正就算能放进，也是同一个候选值）。
  • 如果$E_{min}$也无法放进$E_k$，那么另外两个“较大的信封”自然也无法放进$E_k$，所以也没必要比较了。

按照上面的方法，计算$L_k$的时候，不需要让$E_k$和每一个$E_i(i=1,2,…,k-1)$比较，只需要和现有的每个长度的信封链中最小的末端信封比较就行了。即，比较：

  • 长度1的信封链的最小末端信封
  • 长度2的信封链的最小末端信封
  • ……

注：这个末端信封的$w$、$h$和所属信封链的长度没有任何单调一致性。

下图中，$w_A<w_B$，但$L_A>L_B$

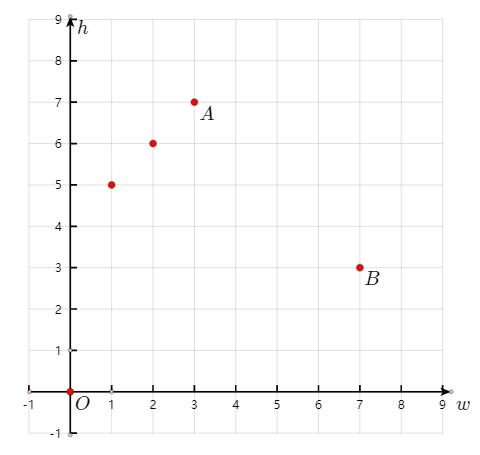
w小的L大.png

下图中，$h_B<w_A$，但$L_B>L_A$

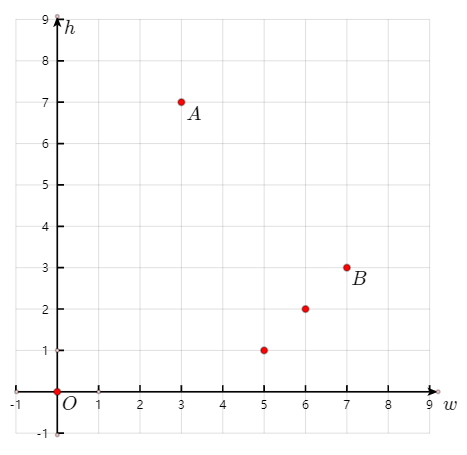
h小的L大.png

优化效果：时间复杂度从$O(N^2)$降低到$O(lN)$，其中$l$是最终答案（最长信封链长度）。

2.2.1. 佯谬：何为最小？

对于一般的LIS问题，上面的优化DP很容易实现。问题是，现在的信封套娃问题包含两个尺寸。这就意味着对于一个给定的信封链长度，很可能没有无可争议的唯一的“最小”末端信封。

例如有3个信封$E_1=(1,1)$、$E_2=(2,3)$、$E_3=(3,2)$。很明显有两个长度2的信封链：

  • (1,1), (2,3)
  • (1,1), (3,2)

两个信封链的末端信封分别是$(2,3)$和$(3,2)$，两者的宽和高的大小关系相反。如下图。

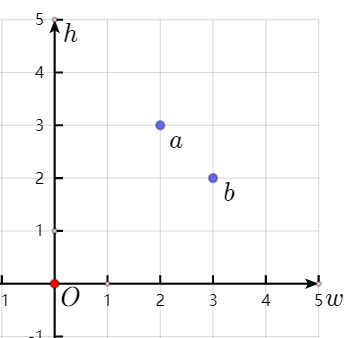
何为最小.png

谁可以作为长度2的信封链的“最小信封”呢？

这不是一个可以忽略的问题。假设除了上面3个信封外还有第四个信封$E_4=(3,4)$，那么：

  • 如果“长度2的信封链的最小末端信封”是$(2,3)$，那么$E_4$就能包裹住它，从而$L_4=L_3+1=2+1=3$。
  • 而如果“长度2的信封链的最小末端信封”是$(3,2)$，很明显$E_4$不能包裹住它，于是$E_4$就只能接在$E_1=(1,1)$的后面，形成$L_4=2$的结果。

2.2.2. 佯谬的解决

在这道题的标准算法里，用了一个很简单的方法。下面先讲述这个方法，然后再解释这个方法为什么能解决“何为最小”佯谬。

这个方法就是：

  • 在最开始排序的时候，对于每个信封$(w_i, h_i)$，优先按照$w$从小到大排序；但当$w$相同的时候，按照$h$从大到小排序。
  • 两个长度相同的信封链，其末端信封的“大小”以末端信封的$h$值为准。如果$h$相同，则哪一个都行。

下图的数字表示排序后的各信封的顺序。

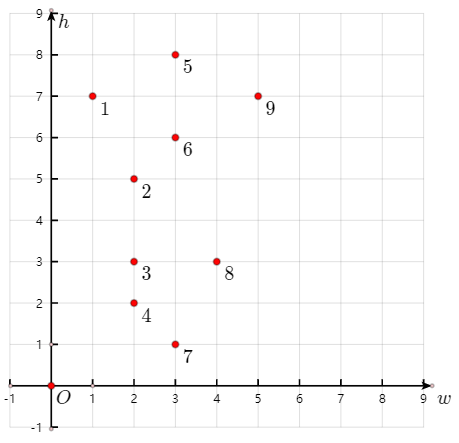
排序后的遍历顺序.png

显然，这个方法算是强行规定了$w$和$h$大小关系相反时两个末端信封的大小关系。为什么这种规定是正确的呢？下面给出证明。

2.2.3. 佯谬解决方案正确性的证明

现有两个长度相同的信封链的末端信封$E_a$和$E_b$，各自的尺寸是$(w_a, h_a)$和$(w_b, h_b)$。

  • 如果两个信封中$w$和$h$值都完全相同，则选哪一个信封都没区别。
  • 如果两个信封中$w$和$h$值之一对应相同，则信封的大小就以另一个不相同的参数的大小关系为准。
  • 如果两个信封中$w$和$h$值的大小关系严格一致（比如$w_a<w_b$且$h_a<h_b$），那么大小关系就确定了。
  • 下面讨论$w_a<w_b$且$h_a>h_b$的情形。

这种情况下，由于$E_a$必定排在$E_b$前面，那么计算$L_b$时，发现$L_b=L_a$且$h_b<h_a$，于是$E_b$就成为了该信封链长度的“最小末端信封”。现在只需要确认这种方式不会让后续的$E_k$错过最长信封链。

由于$E_k$排在$E_b$后面，这说明：

  • 要么$w_k=w_b>w_a$且$h_k<h_b$：由于$h_b<h_a$所以$h_k<h_a$，这时$E_k$既不能包裹$E_a$又不能包裹$E_b$。
  • 要么$w_k>w_b>w_a$。此时关键就是比较$h$值。由于$h_b$还比$h_a$小，$h_k$只需要和$h_b$比较就行。所以此时用$E_b$作为“最小末端信封”不会错过最长信封链。

综上，佯谬解决。经过优先升序$w$、$w$相等再降序$h$的排序后，最小末端信封只需要比较$h$，就不会错过对最长信封链的搜索。

2.3. 再进一步优化DP

在上面的算法中，我们已经计算出了：

  • 长度1的信封链的中$h$最小的末端信封$E_{end}^1$。
  • 长度2的信封链的中$h$最小的末端信封$E_{end}^2$。
  • ……
  • 长度$l$的信封链的中$h$最小的末端信封$E_{end}^l$。（目前最长的信封链的长度是$l$）

当我们用$E_k$去比较这一系列的末端信封时，其实只需要比较$h$值，而不需要比较$w$值。

这意味着，我们不需要保存每个长度的信封链的末端信封的两个值$(w,h)$，只需要保存末端信封的$h$即可。

优化效果：这个优化不仅节约了一半的空间，而且让$E_k$去和这些末端信封作比较的时候无需关心$w$值。

2.3.1. 又一个佯谬？

看到这里可能您有些迷惑，因为按照排序规则，$E_k$的$w$肯定是大于或等于上述末端信封的$w$的。大于也就罢了，万一$w_k$等于某个末端信封的$w$，“不比较$w$”岂不是会让$E_k$接在其不能包裹的末端信封之后？因为“包裹”要求$w_k$严格大于所接的末端信封的$w$。

其实并不会。

2.3.2. 佯谬解决

如果$w_k$真的和某个已有的末端信封$E_{end}^x$的$w$相等。那么由于$E_k$晚于$E_{end}^x$出现，就说明$E_k$的$h$必定小于$E_{end}^x$的$h$（还是因为那个排序规则：$w$相同时降序排列$h$）。此时$h$值的大小关系就决定了算法不可能将$E_k$接在$E_{end}^x$之后。

2.3.3. 可视化证明

下图给出了当前信封$E_k$可能的信封链的前驱范围（大致如此，实际上扇形半径无限长，且位于k下方的那条扇形终点半径是几乎垂直向下但不完全垂直向下的）。

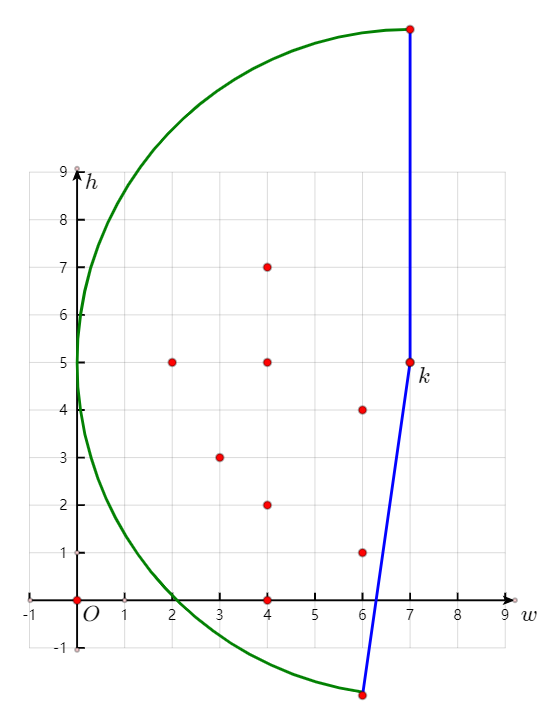
前驱范围.png

对于点$k$，扇形范围中的所有点在排序时都会出现在$k$的前面。

现在设想扇形中的点有若干点同是长度$l$的信封链的终点。如果只能这若干点中的一个，应该保留哪一个呢？

答案是：保留$h$最小的那个$E_{minh}$就行了。

  • 如果$E_k$能接在$E_{minh}$之后，那么$L_k=$L_{minh}}+1$；
  • 如果$E_k$不能接在$E_{minh}$之后，那么也不能接在有相同信封链长度的其他信封后面。

2.4. 再再进一步优化DP

现在我们有了一个数组：

  • 长度1的信封链的中$h$最小的末端信封的$h$值$h_{end}^1$。
  • 长度2的信封链的中$h$最小的末端信封的$h$值$h_{end}^2$。
  • ……
  • 长度$l$的信封链的中$h$最小的末端信封的$h$值$h_{end}^l$。（目前最长的信封链的长度是$l$）

这个数组是严格单调递增的。

证明：因为长度$s$的信封链的前$s-1$个信封就是长度$s-1$的信封链，而这个“前缀信封链”的末端信封的$h$值必然小于$h_{end}^s$。如果$h_{end}^{s-1}≥h_{end}^s$，则“前缀信封链”的末端信封的$h$值就更有资格作为$h_{end}^{s-1}$了。和现状矛盾。

那么，为$E_k$寻找“能包裹的最长信封链的末端信封”就转化成了为$h_k$寻找最大且严格小于$h_k$的$h_{end}^i(i=1,2,…,l)$。在严格递增数组里寻找这样的值，自然是使用二分查找。

这样，计算$L_k$的时间复杂度就变成了$O(logl)$。

于是完整的算法的时间复杂度就变成了$O(Nlogl)$，其中$l$是整个数据集中的最长信封链的长度。显然$l<N$，所以也可以认为算法的时间复杂度是$O(NlogN)$。

优化效果：时间复杂度降低到$O(NlogN)$。

2.5. 算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution {
    static bool compareEnvelopes(vector<int> &a, vector<int> &b) {
        if (a[0] == b[0]) {
            return a[1] > b[1];
        }
        return a[0] < b[0];
    }
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        sort(envelopes.begin(), envelopes.end(), compareEnvelopes);
        vector<int> minHeight(1, INT_MIN); // [i]的值表示所有长度i的信封链的末端信封的最小h值。[0]无意义。
        for (int i = 0; i < envelopes.size(); i++) {
            auto &now = envelopes[i];
            int targetPos = search(minHeight, now[1]);
            if (targetPos + 1 >= minHeight.size()) {
                minHeight.push_back(now[1]);
            } else {
                minHeight[targetPos + 1] = min(minHeight[targetPos + 1], now[1]);
            }
        }
        return minHeight.size() - 1;
    }
    int search(vector<int> &minHeight, int nowHeight) {
        int begin = 0;
        int end = minHeight.size();
        while (begin + 1 < end) {
            int mid = (begin + end) / 2;
            if (minHeight[mid] >= nowHeight) {
                end = mid;
            } else {
                begin = mid;
            }
        }
        return begin;
    }
};